A digital signature in its simplest description is a hash (SHA1, MD5, etc.) of the data (file, message, etc.) that is subsequently encrypted with the signer’s private key. Since that is something only the signer has (or should have) that is where the trust comes from. EVERYONE has (or should have) access to the signer’s public key.

So, to validate a digital signature, the recipient

1. Calculates a hash of the same data (file, message, etc.),
2. Decrypts the digital signature using the sender’s PUBLIC key, and
3. Compares the 2 hash values.

Sender – Alice is sending a digitally signed but not encrypted message to Receiver – Bob

1. Sender generates a message digest of the original plaintext message using a secure hash function like SHA3-512.
2. Sender then encrypts the message digest using her private key. The output is the digital signature.
3. Sender appends the digital signature to the plaintext message.
4. Sender then sends the appended message to Receiver. Sender sends digital signature + Plain Text Message + Certificate with Public Key
5. Receiver removes the digital signature from the appended message and decrypts it with the public key of Sender.
6. Receiver calculates the hash of the plaintext message with SHA3-512.
7. Receiver then compares the decrypted message digest he received from Sender with the message digest Receiver computed. If the two digests match, he can be assured that the message he received was sent by Sender.

The digital signature process does not provide any privacy by itself. It only ensures that the cryptographic goals of authentication, integrity, and nonrepudiation are met. If Sender wants to ensure the privacy of her message to Receiver, she could encrypt the appended message generated in step 3 with the public key of Receiver. Receiver then would need to first decrypt the encrypted message with his private key before continuing with step 5.

What Sender Does?

Note: In the above step the hash is encrypted digitally signed using private key.In the side of the receiver public key should be used to decrypt hash for verification

What Receiver Does?

Encryption vs Digital Signature

In Encryption we use receivers public key to encrypt the message whereas when we digitally sign we use senders private to encrypt the hashed text(which is nothing again message we would like to send)

Encryption
Encryption is the act of converting plain text to cipher text. Cipher text is basically text that has been scrambled into non-readable format using an algorithm – called a cipher.

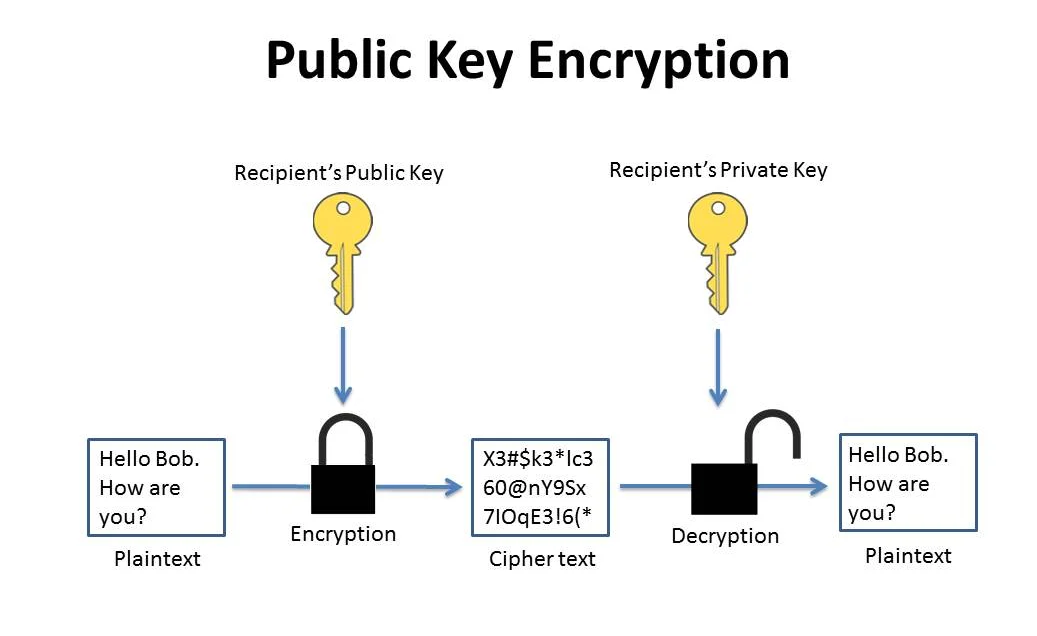
Public key encryption uses public/private key pairs. If you want me to send you an encrypted message, you send me your public key, which I import into my encryption software. I encrypt the message with your public key. When you receive the message, you decrypt it with your private key. Even though your public key can be freely distributed and used to encrypt messages addressed to you, these encrypted messages can only be decrypted with your own private key. This private key must always be kept secret. Data encrypted with the public key can only be decrypted with its corresponding private key. This is what happens in Brower Server Communication

Digital Signature
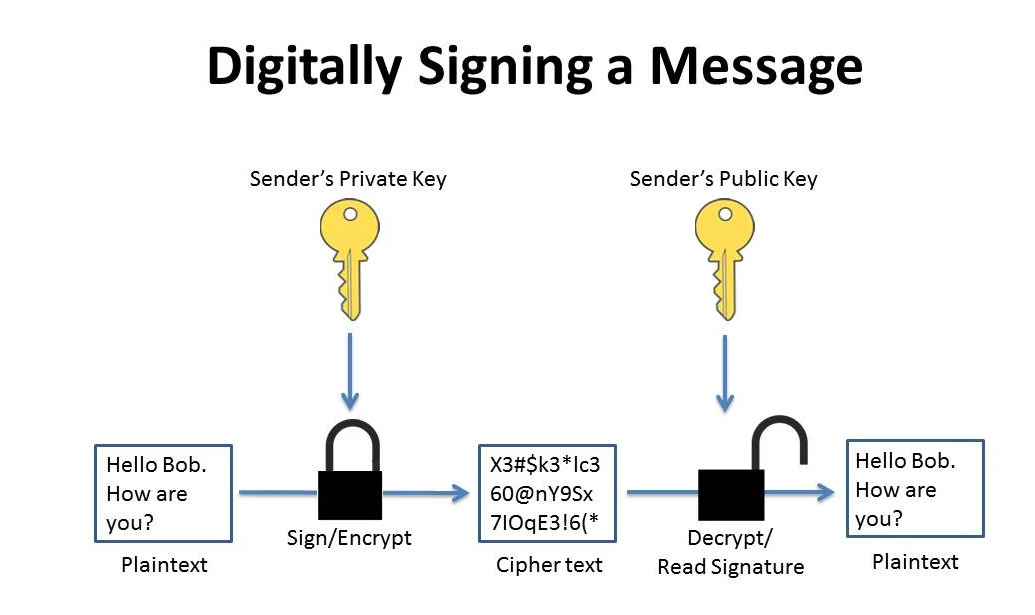
Message signing, on the other hand, uses the sender’s private key to sign the message, and his public key is used to read the signature. Message signing helps ensure data integrity, message authentication, and non-repudiation. For example, if John wants to digitally sign a message to Bob, he uses his private key to sign the message, and sends it (along with his public key if it hasn’t already been sent) to Bob. John’s public key is the only key that can verify the message signature.

In RSA crypto, when you generate a key pair, it’s completely arbitrary which one you choose to be the public key, and which is the private key. If you encrypt with one, you can decrypt with the other – it works in both directions. It is fairly simple to see how you can encrypt a message with the receiver’s public key so that the receiver can decrypt it with their private key.

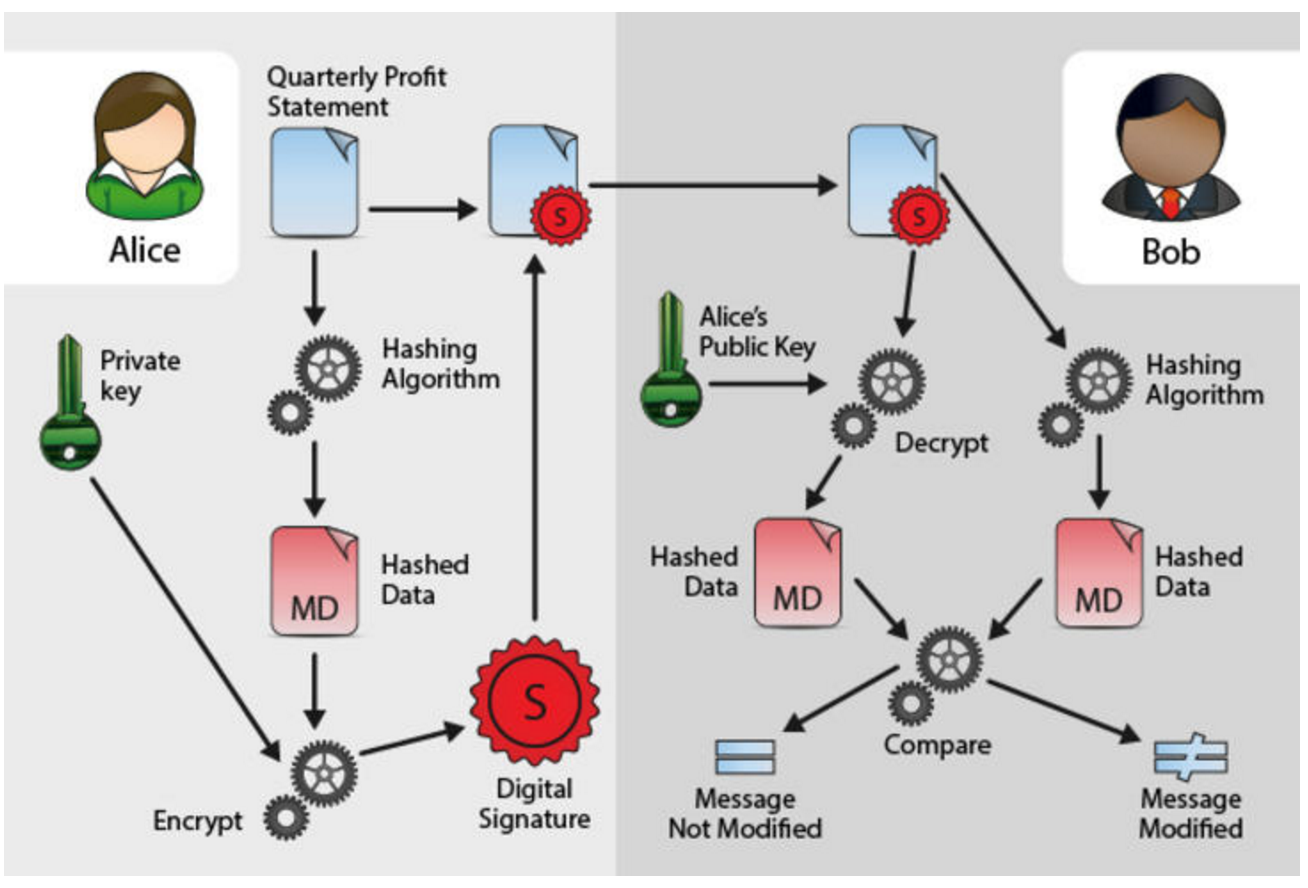
A signature is proof that the signer has a private key that matches some public key. To do this, it would be enough to encrypt the message with that sender’s private key and include the encrypted version alongside the plaintext version. To verify the sender, decrypt the encrypted version, and check that it is the same as the plaintext.

Of course, this means that your message is not secret. Anyone can decrypt it because the public key is well known. But when they do so, they have proved that the creator of the ciphertext has the corresponding private key.

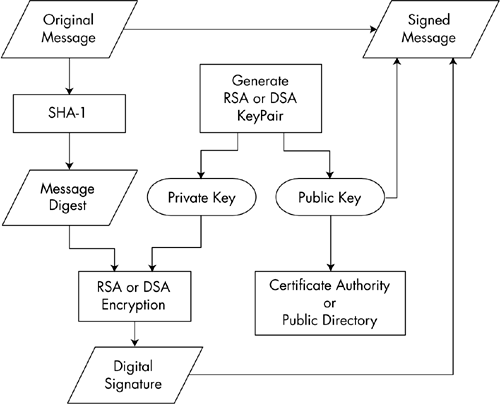
However, this means doubling the size of your transmission – plaintext, and ciphertext together (assuming you want people who aren’t interested in verifying the signature, to read the message). So instead, typically a signature is created by creating a hash of the plaintext. Fake hashes can never be created, so cryptographic hash algorithms such as SHA-2 are used.

• To generate a signature, make a hash from the plaintext, encrypt it with your private key, include it alongside the plaintext.
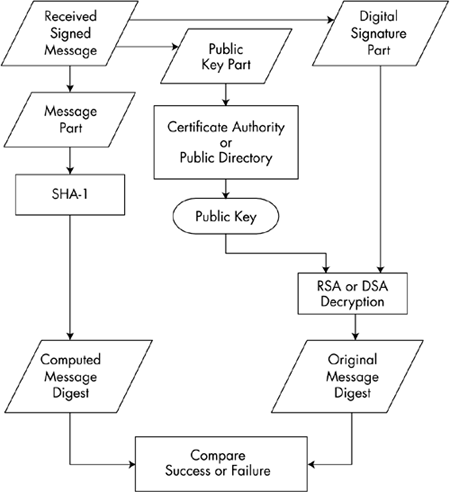
• To verify a signature, make a hash from the plaintext, decrypt the signature with the sender’s public key, check that both hashes are the same.

Encryption and Decryption
Encrytion and Decryption could use same key as in symmetric algorithm or could use different one. Below are the steps for Asymmetric encrytion.

1. Alice wants to send a message to Bob which no one should be able to read.
2. 1. Alice encrypts the message with Bob’s public key and sends it over.
   2. Bob receives the message and decrypts it using his private Key.

   Note that if A wants to send a message to B, A needs to use the Public key of B (which is publicly available to anyone) and neither public nor private key of A comes into the picture here.
   

So if you want to send a message to me you should know and use my public key which I provide to you and only I will be able to decrypt the message since I am the only one who has access to the corresponding private key.

Digitally Signing Message

1. Alice wants to send a message to Bob again. The problem of encrypting the data is solved using the above method.
2. But what if I am sitting between Alice and Bob, introducing myself as ‘Alice’ to Bob and sending my own message to Bob instead of forwarding the one sent by Alice. Even though I can not decrypt and read the original message sent by Alice(that requires access to Bob’s private key) I am hijacking the entire conversation between them.
3. Is there a way Bob can confirm that the messages he is receiving are actually sent by Alice?
4. Alice signs the message with her private key and sends it over. (In practice, what is signed is a hash of the message, e.g. SHA-256 or SHA-512.)
   Bob receives it and verifies it using Alice’s public key. Since Alice’s public key successfully verified the message, Bob can conclude that the message has been signed by Alice.