What is Asymptotic Analysis
Asymptotic Analysis, we evaluate the performance of an algorithm in terms of input size (we don’t measure the actual running time). We calculate, how does the time (or space) taken by an algorithm increases with the input size.
Asymptotic Analysis is not perfect, but that’s the best way available for analyzing algorithms. For example, say there are two sorting algorithms that take 1000nLogn and 2nLogn time respectively on a machine. Both of these algorithms are asymptotically same (order of growth is nLogn). So, With Asymptotic Analysis, we can’t judge which one is better as we ignore constants in Asymptotic Analysis. Also, in Asymptotic analysis, we always talk about input sizes larger than a constant value. It might be possible that those large inputs are never given to your software and an algorithm which is asymptotically slower, always performs better for your particular situation. So, you may end up choosing an algorithm that is Asymptotically slower but faster for your software.
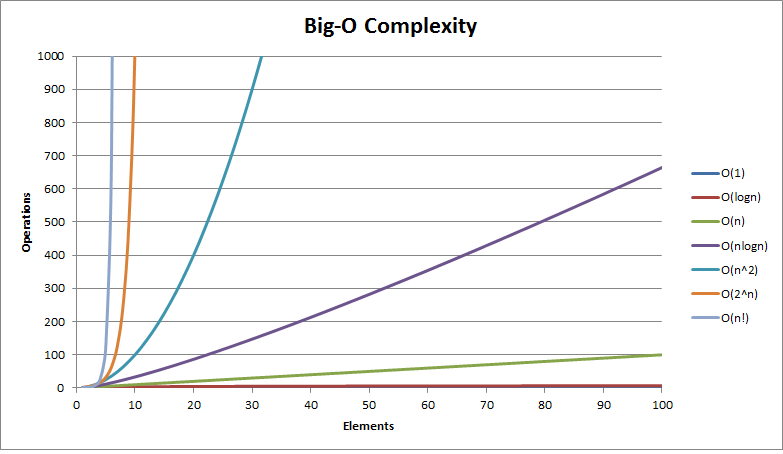
Increasing Order of Growth
| Time Complexity | Name | Example |
|---|---|---|
| 1 | Constant | Adding Element to the Front oif Linked List |
| logn | Logarithmic | Finding the element in the Sorted Array |
| n | Linear | Finding an element in an unserted Array |
| nLogn | Linear Logarithmic | Sorting n items by divide and conquer technique |
| n² | Quadriatic | Shortest Path between two nodes in a graph |
| n³ | Cubic | Matrix Multiplication |
| 2n | Exponential | The Towers of Hanoi Problem |
Let’s take a simple java code which looks for a number in an array
public class LinearSearch
{
// Linearly search x in arr[]. If x is present then return the index,
static int search(int arr[], int n, int x) {
int i;
for (i = 0; i < n; i++) {
if (arr[i] == x) {
return i;
}
}
return -1;
}
public static void main(String[] args)
{
int arr[] = {41, 10, 40, 15};
int x = 40;
int n = arr.length;
System.out.printf("%d is present at index %d", x, search(arr, n, x));
}
}
In the above scenario we have
Worst Case – O Notation(Big O Notation) – In the Worst case we calculate the Upper bound of the algorithm with the worst possible input. In our case it is O(n) if the element is found as last item of the array. The Big O notation defines an upper bound of an algorithm, it bounds a function only from above. For example, consider the case of Insertion Sort. It takes linear time in the best case and quadratic time in the worst case. We can safely say that the time complexity of Insertion sort is O(n^2)
Best Case – Ω Notation(Omega Notation) – In the Best case we calculate the lower bound of the algorithm with the best possible input. In our case it is O(1) if the element is found in as first item of the array.
AverageCase- Θ Notation(Theta Notation) – average case analysis, we take all possible inputs and calculate computing time for all of the inputs. Sum all the calculated values and divide the sum by total number of inputs
- A case is a class of inputs for which you consider your algorithm’s performance.
- the best case is the input that minimizes the function and the worst case is the input that maximizes the function
- An algorithm always have worst case, best case and average case
- Each case again has an upper bound, lower bound.Bounds are functions that we use to compare against a given algorithm’s function.
- An upper bound is a function that sits on top of another function. A lower bound is a function that sits under the other function. When we talk about Big O and Big Omega, we don’t care if the bounds are ALWAYS above or below the other function
- When we talk about worst case we would be always interested in upper bound and when we talk about Best Case we are always interested in lower bound.Because of this Worst Case and upper bound are used interchangably and vice versa.
- Worst Case Upper Bound: We are often interested in finding a tight upper bound on the worst case, because then we know how poorly our algorithm can run in the worst of times. Insertion sort’s worst case is a list that is completely out of order (i.e. completely reversed from its correct order). Every time we see a new item, we have to move it to the start of the list, pushing all subsequent items forward (which is a linear time operation, and doing it a linear number of times leads to quadratic behavior). However, we still know that this insertion behavior will be O(n2) in the worst case, acting as a tight upper bound for the worst case.
- Best Case Lower Bound: Insertion Sort works by walking through the list, and inserting any out-of-order it comes across in the right place. If the list is sorted, it will only need to walk through the list once without doing any inserts. This means that the tightest lower bound of the best case is Ω(n). You cannot do better than that without sacrificing correctness, because you still need to be able to walk through the list (linear time). However, the lower bound for the best case is better than the lower bound for the worst case!
- Worst Case Lower Bound: The classic example here is comparison-based sorting, which is famously known to be Ω(n log(n)) in the worst case. No matter what algorithm you devise, I can pick a set of worst-case inputs whereby the tightest lower bound function is log-linear. You cannot make an algorithm that beats that bound for the worst case, and you shouldn’t bother trying. It’s the basement of sorting. Of course, there are many lower bounds for the worst case: constant, linear, and sublinear are all lower bounds. But they are not useful lower bounds, because there the log-linear lower bound is the tightest one.
- Best Case Upper Bound: What’s the worst our algorithm can do in the best of times? In example before of finding an element in a list, where the first element was our desired element, the upper bound is O(1). In the worst case it was linear, but in the best case, the worst that can happen is that it’s still constant. This particular idea isn’t usually as important as Worst Case Upper Bound, in my opinion, because we’re usually more concerned with dealing with the worst case, not the best case.
Legends
![]()
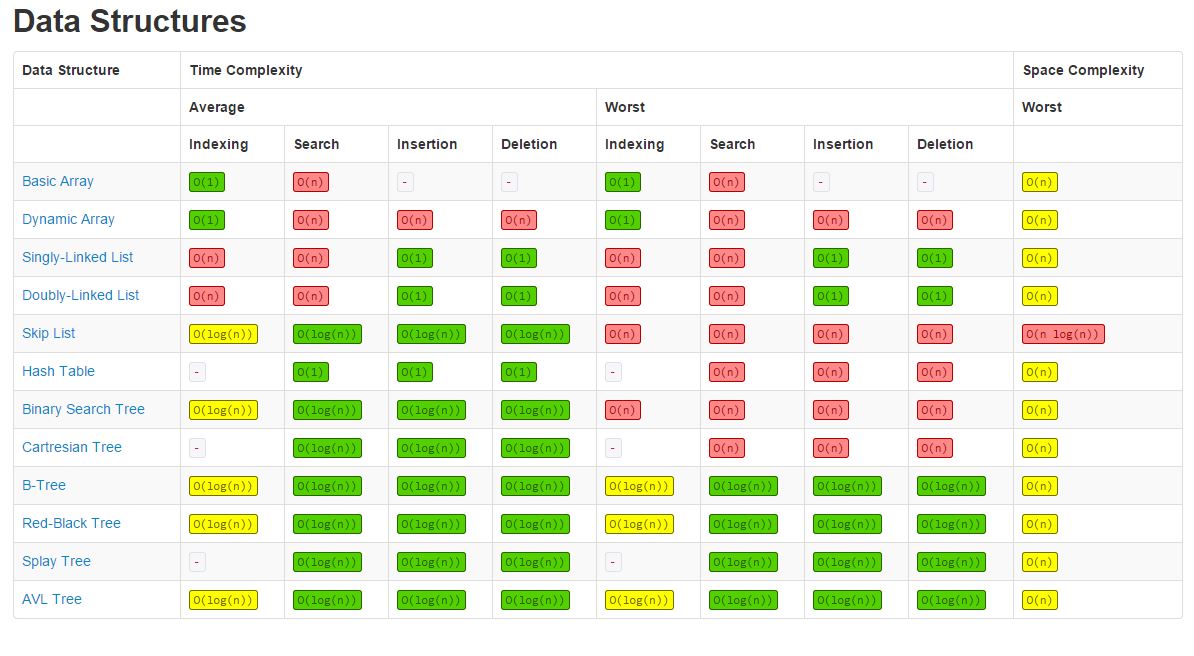
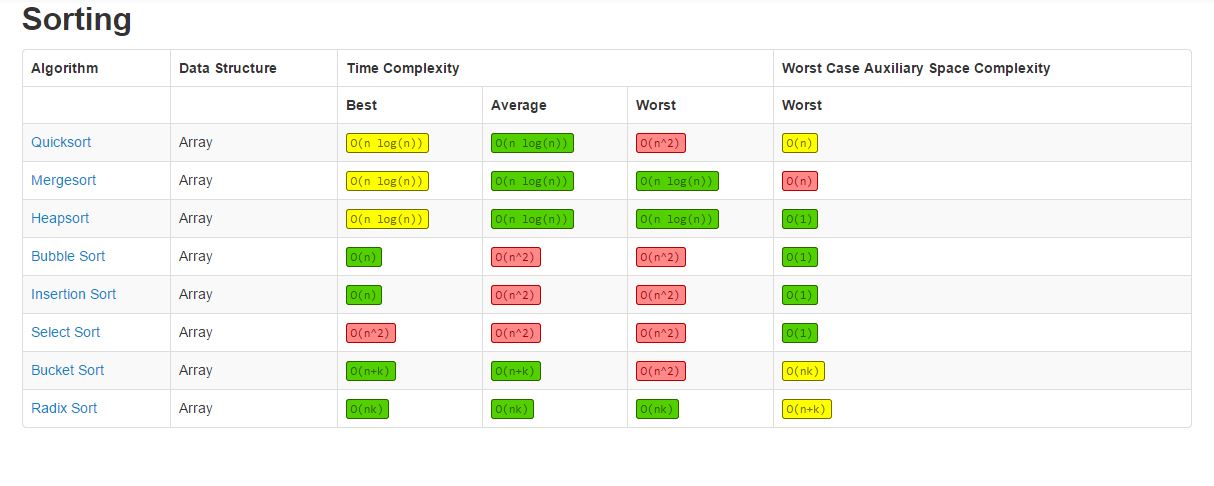
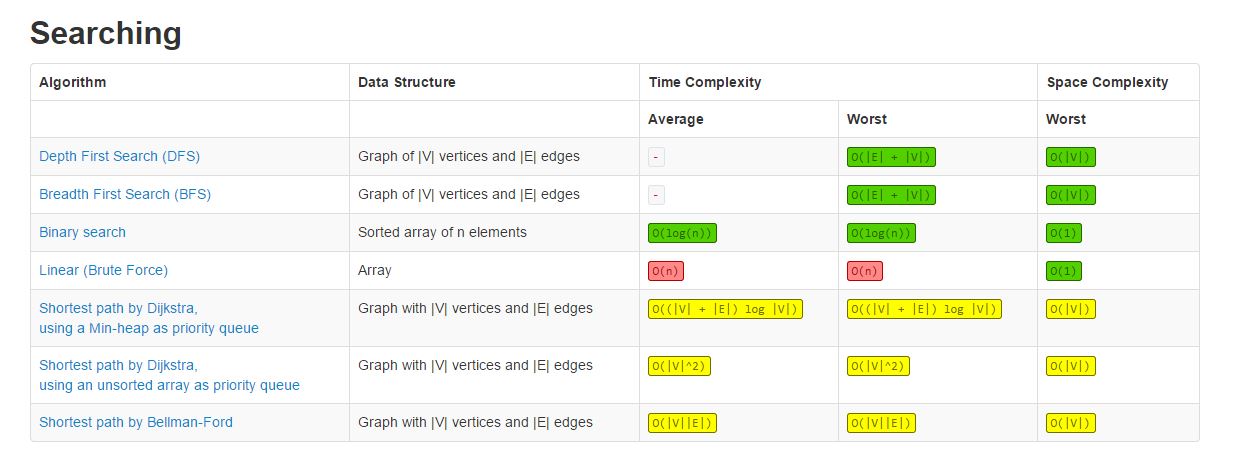

Time Complexity